One of the more exciting applications of decentralized computing that have aroused a considerable amount of interest in the past year is the concept of an incentivized decentralized online file storage system. Currently, if you want your files or data securely backed up “in the cloud”, you have three choices – (1) upload them to your own servers, (2) use a centralized service like Google Drive or Dropbox or (3) use an existing decentralized file system like Freenet. These approaches all have their own faults; the first has a high setup and maintenance cost, the second relies on a single trusted party and often involves heavy price markups, and the third is slow and very limited in the amount of space that it allows each user because it relies on users to volunteer storage. Incentivized file storage protocols have the potential to provide a fourth way, providing a much higher quantity of storage and quality of service by incentivizing actors to participate without introducing centralization.
A number of platforms, including StorJ, Maidsafe, to some extent Permacoin, and Filecoin, are attempting to tackle this problem, and the problem seems simple in the sense that all the tools are either already there or en route to being built, and all we need is the implementation. However, there is one part of the problem that is particularly important: how do we properly introduce redundancy? Redundancy is crucial to security; especially in a decentralized network that will be highly populated by amateur and casual users, we absolutely cannot rely on any single node to stay online. We could simply replicate the data, having a few nodes each store a separate copy, but the question is: can we do better? As it turns out, we absolutely can.
Merkle Trees and Challenge-Response Protocols
Before we get into the nitty gritty of redundancy, we will first cover the easier part: how do we create at least a basic system that will incentivize at least one party to hold onto a file? Without incentivization, the problem is easy; you simply upload the file, wait for other users to download it, and then when you need it again you can make a request querying for the file by hash. If we want to introduce incentivization, the problem becomes somewhat harder – but, in the grand scheme of things, still not too hard.
In the context of file storage, there are two kinds of activities that you can incentivize. The first is the actual act of sending the file over to you when you request it. This is easy to do; the best strategy is a simple tit-for-tat game where the sender sends over 32 kilobytes, you send over 0.0001 coins, the sender sends over another 32 kilobytes, etc. Note that for very large files without redundancy this strategy is vulnerable to extortion attacks – quite often, 99.99% of a file is useless to you without the last 0.01%, so the storer has the opportunity to extort you by asking for a very high payout for the last block. The cleverest fix to this problem is actually to make the file itself redundant, using a special kind of encoding to expand the file by, say, 11.11% so that any 90% of this extended file can be used to recover the original, and then hiding the exact redundancy percentage from the storer; however, as it turns out we will discuss an algorithm very similar to this for a different purpose later, so for now, simply accept that this problem has been solved.
The second act that we can incentivize is the act of holding onto the file and storing it for the long term. This problem is somewhat harder – how can you prove that you are storing a file without actually transferring the whole thing? Fortunately, there is a solution that is not too difficult to implement, using what has now hopefully established a familiar reputation as the cryptoeconomist’s best friend: Merkle trees.
Well, Patricia Merkle might be better in some cases, to be precise. Athough here the plain old original Merkle will do.
n = 2^kfor some
k(the padding step is avoidable, but it makes the algorithm simpler to code and explain). Then, we build the tree. Rename the
nchunks that we received
chunk(n)to
chunk(2n-1), and then rebuild chunks
1to
n-1with the following rule:
chunk(i) = sha3((chunk(2*i), chunk(2*i+1))). This lets you calculate chunks
n/2to
n-1, then
n/4to
n/2 - 1, and so forth going up the tree until there is one “root”,
chunk(1).
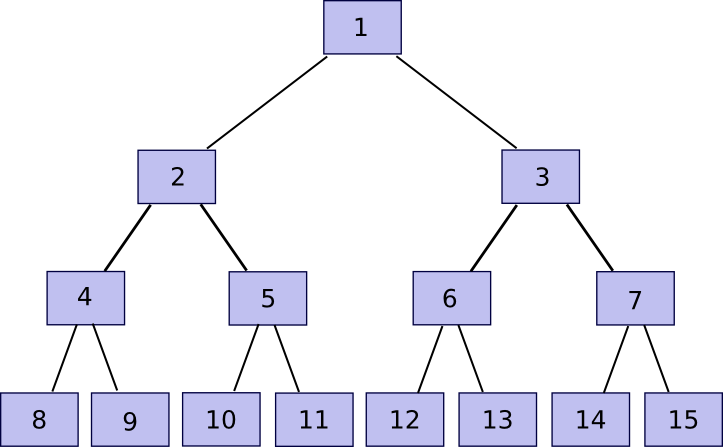
Now, note that if you store only the root, and forget about chunk(2) … chunk(2n-1), the entity storing those other chunks can prove to you that they have any particular chunk with only a few hundred bytes of data. The algorithm is relatively simple. First, we define a function partner(n) which gives n-1 if n is odd, otherwise n+1 – in short, given a chunk find the chunk that it is hashed together with in order to produce the parent chunk. Then, if you want to prove ownership of chunk(k) with n <= k <= 2n-1 (ie. any part of the original file), submit chunk(partner(k)), chunk(partner(k/2)) (division here is assumed to round down, so eg. 11 / 2 = 5), chunk(partner(k/4)) and so on down to chunk(1), alongside the actual chunk(k). Essentially, we’re providing the entire “branch” of the tree going up from that node all the way to the root. The verifier will then take chunk(k) and chunk(partner(k)) and use that to rebuild chunk(k/2), use that and chunk(partner(k/2)) to rebuild chunk(k/4) and so forth until the verifier gets to chunk(1), the root of the tree. If the root matches, then the proof is fine; otherwise it’s not.
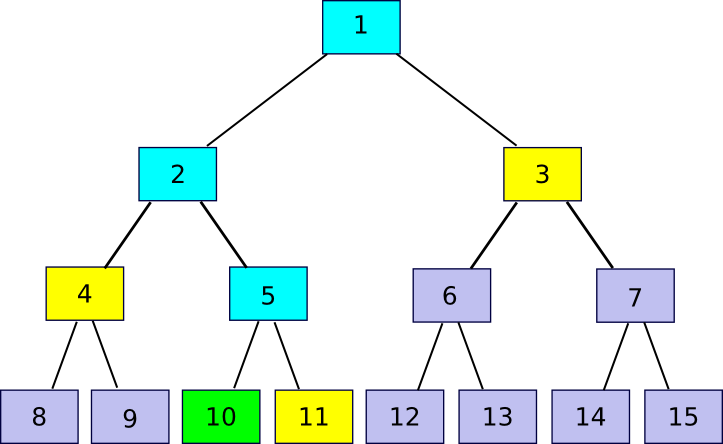
11 = partner(10)), 4 (
4 = partner(10/2)) and 3 (
3 = partner(10/4)). The verification process involves starting off with chunk 10, using each partner chunk in turn to recompute first chunk 5, then chunk 2, then chunk 1, and seeing if chunk 1 matches the value that the verifier had already stored as the root of the file.
Note that the proof implicitly includes the index – sometimes you need to add the partner chunk on the right before hashing and sometimes on the left, and if the index used to verify the proof is different then the proof will not match. Thus, if I ask for a proof of piece 422, and you instead provide even a valid proof of piece 587, I will notice that something is wrong. Also, there is no way to provide a proof without ownership of the entire relevant section of the Merkle tree; if you try to pass off fake data, at some point the hashes will mismatch and the final root will be different.
Now, let’s go over the protocol. I construct a Merkle tree out of the file as described above, and upload this to some party. Then, every 12 hours, I pick a random number in (0, 2^k-1) and submit that number as a challenge. If the storer replies back with a Merkle tree proof, then I verify the proof and if it is correct send 0.001 BTC (or ETH, or storjcoin, or whatever other token is used). If I receive no proof or an invalid proof, then I do not send BTC. If the storer stores the entire file, they will succeed 100% of the time, if they store 50% of the file they will succeed 50% of the time, etc. If we want to make it all-or-nothing, then we can simply require the storer to solve ten consecutive proofs in order to get a reward. The storer can still get away with storing 99%, but then we take advantage of the same redundant coding strategy that I mentioned above and will describe below to make 90% of the file sufficient in any case.
One concern that you may have at this point is privacy – if you use a cryptographic protocol to let any node get paid for storing your file, would that not mean that your files are spread around the internet so that anyone can potentially access them? Fortunately the answer to this is simple: encrypt the file before sending it out. From this point on, we’ll assume that all data is encrypted, and ignore privacy because the presence of encryption resolves that issue almost completely (the “almost” being that the size of the file, and the times at which you access the file, are still public).
Looking to Decentralize
So now we have a protocol for paying people to store your data; the algorithm can even be made trust-free by putting it into an Ethereum contract, using
block.prevhash as a source of random data to generate the challenges. Now let’s go to the next step: figuring out how to decentralize the storage and add redundancy. The simplest way to decentralize is simple replication: instead of one node storing one copy of the file, we can have five nodes storing one copy each. However, if we simply follow the naive protocol above, we have a problem: one node can pretend to be five nodes and collect a 5x return. A quick fix to this is to encrypt the file five times, using five different keys; this makes the five identical copies indistinguishable from five different files, so a storer will not be able to notice that the five files are the same and store them once but claim a 5x reward.
But even here we have two problems. First, there is no way to verify that the five copies of the file are stored by five separate users. If you want to have your file backed up by a decentralized cloud, you are paying for the service of decentralization; it makes the protocol have much less utility if all five users are actually storing everything through Google and Amazon. This is actually a hard problem; although encrypting the file five times and pretending that you are storing five different files will prevent a single actor from collecting a 5x reward with 1x storage, it cannot prevent an actor from collecting a 5x reward with 5x storage, and economies of scale mean even that situation will be desirable from the point of view of some storers. Second, there is the issue that you are taking a large overhead, and especially taking the false-redundancy issue into account you are really not getting that much redundancy from it – for example, if a single node has a 50% chance of being offline (quite reasonable if we’re talking about a network of files being stored in the spare space on people’s hard drives), then you have a 3.125% chance at any point that the file will be inaccessible outright.
There is one solution to the first problem, although it is imperfect and it’s not clear if the benefits are worth it. The idea is to use a combination of proof of stake and a protocol called “proof of custody” – proof of simultaneous possession of a file and a private key. If you want to store your file, the idea is to randomly select some number of stakeholders in some currency, weighting the probability of selection by the number of coins that they have. Implementing this in an Ethereum contract might involve having participants deposit ether in the contract (remember, deposits are trust-free here if the contract provides a way to withdraw) and then giving each account a probability proportional to its deposit. These stakeholders will then receive the opportunity to store the file. Then, instead of the simple Merkle tree check described in the previous section, the proof of custody protocol is used.
The proof of custody protocol has the benefit that it is non-outsourceable – there is no way to put the file onto a server without giving the server access to your private key at the same time. This means that, at least in theory, users will be much less inclined to store large quantities of files on centralized “cloud” computing systems. Of course, the protocol accomplishes this at the cost of much higher verification overhead, so that leaves open the question: do we want the verification overhead of proof of custody, or the storage overhead of having extra redundant copies just in case?
M of N
Regardless of whether proof of custody is a good idea, the next step is to see if we can do a little better with redundancy than the naive replication paradigm. First, let’s analyze how good the naive replication paradigm is. Suppose that each node is available 50% of the time, and you are willing to take 4x overhead. In those cases, the chance of failure is
0.5 ^ 4 = 0.0625 – a rather high value compared to the “four nines” (ie. 99.99% uptime) offered by centralized services (some centralized services offer five or six nines, but purely because of Talebian black swan considerations any promises over three nines can generally be considered bunk; because decentralized networks do not depend on the existence or actions of any specific company or hopefully any specific software package, however, decentralized systems arguably actually can promise something like four nines legitimately). If we assume that the majority of the network will be quasi-professional miners, then we can reduce the unavailability percentage to something like 10%, in which case we actually do get four nines, but it’s better to assume the more pessimistic case.
What we thus need is some kind of M-of-N protocol, much like multisig for Bitcoin. So let’s describe our dream protocol first, and worry about whether it’s feasible later. Suppose that we have a file of 1 GB, and we want to “multisig” it into a 20-of-60 setup. We split the file up into 60 chunks, each 50 MB each (ie. 3 GB total), such that any 20 of those chunks suffice to reconstruct the original. This is information-theoretically optimal; you can’t reconstruct a gigabyte out of less than a gigabyte, but reconstructing a gigabyte out of a gigabyte is entirely possible. If we have this kind of protocol, we can use it to split each file up into 60 pieces, encrypt the 60 chunks separately to make them look like independent files, and use an incentivized file storage protocol on each one separately.
Now, here comes the fun part: such a protocol actually exists. In this next part of the article, we are going to describe a piece of math that is alternately called either “secret sharing” or “erasure coding” depending on its application; the algorithm used for both those names is basically the same with the exception of one implementation detail. To start off, we will recall a simple insight: two points make a line.
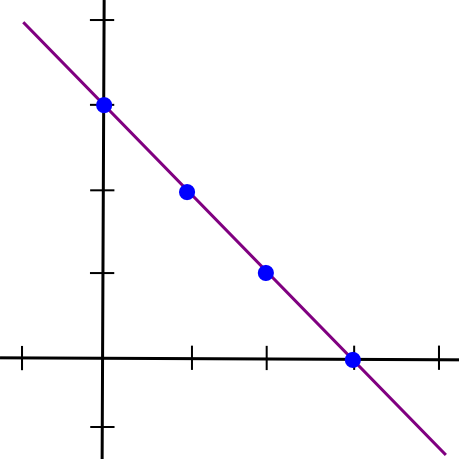
x = 1and the second half as the y coordinate of the line at
x = 2, draw the line, and take points at
x = 3,
x = 4, etc. Any two pieces can then be used to reconstruct the line, and from there derive the y coordinates at
x = 1and
x = 2 to get the file back.
Mathematically, there are two ways of doing this. The first is a relatively simple approach involving a system of linear equations. Suppose that we file we want to split up is the number “1321”. The left half is 13, the right half is 21, so the line joins (1, 13) and (2, 21). If we want to determine the slope and y-intercept of the line, we can just solve the system of linear equations:
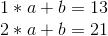
Subtract the first equation from the second, and you get:
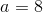
And then plug that into the first equation, and get:
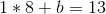
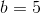
So we have our equation, y = 8 * x + 5. We can now generate new points: (3, 29), (4, 37), etc. And from any two of those points we can recover the original equation.
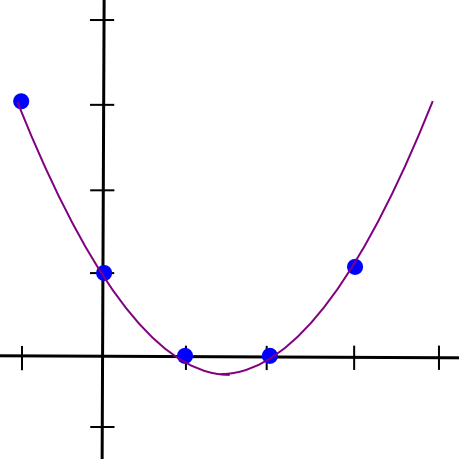
Now, let’s go one step further, and generalize this into m-of-n. As it turns out, it’s more complicated but not too difficult. We know that two points make a line. We also know that three points make a parabola:
x = 1, 2, 3, and take further points on the parabola as additional pieces. If we want 4-of-n, we use a cubic polynomial instead. Let’s go through that latter case; we still keep our original file, “1321”, but we’ll split it up using 4-of-7 instead. Our four points are
(1, 1),
(2, 3),
(3, 2),
(4, 1). So we have:
Eek! Well, let’s, uh, start subtracting. We’ll subtract equation 1 from equation 2, 2 from 3, and 3 from 4, to reduce four equations to three, and then repeat that process again and again.
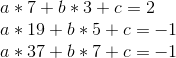
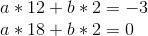
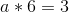
So a = 1/2. Now, we unravel the onion, and get:
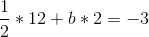
So b = -9/2, and then:
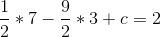
So c = 12, and then:
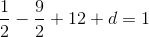
So a = 0.5, b = -4.5, c = 12, d = -7. Here’s the lovely polynomial visualized:
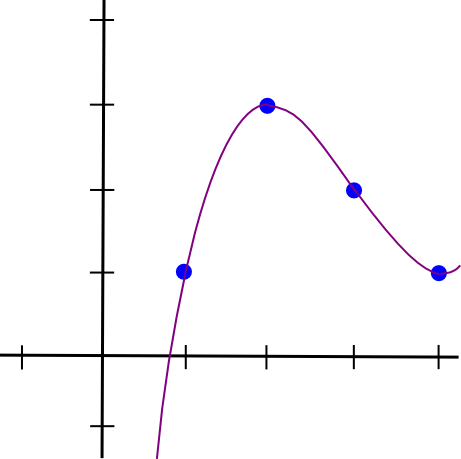
I created a Python utility to help you do this (this utility also does other more advanced stuff, but we’ll get into that later); you can download it here. If you wanted to solve the equations quickly, you would just type in:
> import share > share.sys_solve(((1.0, 1.0, 1.0, 1.0, -1.0), (8.0, 4.0, 2.0, 1.0, -3.0), (27.0, 9.0, 3.0, 1.0, -2.0), (64.0, 16.0, 4.0, 1.0, -1.0))) (0.5, -4.5, 12.0, -7.0)
Note that putting the values in as floating point is necessary; if you use integers Python’s integer division will screw things up.
Now, we’ll cover the easier way to do it, Lagrange interpolation. The idea here is very clever: we come up with a cubic polynomial whose value is 1 at x = 1 and 0 at x = 2, 3, 4, and do the same for every other x coordinate. Then, we multiply and add the polynomials together; for example, to match (1, 3, 2, 1) we simply take 1x the polynomial that passes through (1, 0, 0, 0), 3x the polynomial through (0, 1, 0, 0), 2x the polynomial through (0, 0, 1, 0) and 1x the polynomial through (0, 0, 0, 1) and then add those polynomials together to get the polynomal through (1, 3, 2, 1) (note that I said the polynomial passing through (1, 3, 2, 1); the trick works because four points define a cubic polynomial uniquely). This might not seem easier, because the only way we have of fitting polynomials to points to far is the cumbersome procedure above, but fortunately, we actually have an explicit construction for it:
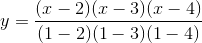
At x = 1, notice that the top and bottom are identical, so the value is 1. At x = 2, 3, 4, however, one of the terms on the top is zero, so the value is zero. Multiplying up the polynomials takes quadratic time (ie. ~16 steps for 4 equations), whereas our earlier procedure took cubic time (ie. ~64 steps for 4 equations), so it’s a substantial improvement especially once we start talking about larger splits like 20-of-60. The python utility supports this algorithm too:
> import share > share.lagrange_interp((1.0, 3.0, 2.0, 1.0), (1.0, 2.0, 3.0, 4.0)) (-7.0, 12.000000000000002, -4.5, 0.4999999999999999)
The first argument is the y coordinates, the second is the x coordinates. Note the opposite order here; the code in the python module puts the lower-order coefficients of the polynomial first. And finally, let’s get our additional shares:
> share.eval_poly_at((-7.0, 12.0, -4.5, 0.5), 5) 3.0 > share.eval_poly_at((-7.0, 12.0, -4.5, 0.5), 6) 11.0 > share.eval_poly_at((-7.0, 12.0, -4.5, 0.5), 7) 28.0
So here immediately we can see two problems. First, it looks like computerized floating point numbers aren’t infinitely precise after all; the 12 turned into 12.000000000000002. Second, the chunks start getting large as we move further out; at x = 10, it goes up to 163. This is somewhat breaking the promise that the amount of data you need to recover the file is the same size as the original file; if we lose x = 1, 2, 3, 4 then you need 8 digits to get the original values back and not 4. These are both serious issues, and ones that we will resolve with some more mathematical cleverness later, but we’ll leave them aside for now.
Even with those issues remaining, we have basically achieved victory, so let’s calculate our spoils. If we use a 20-of-60 split, and each node is online 50% of the time, then we can use combinatorics – specifically, the binomial distribution formula – to compute the probability that our data is okay. First, to set things up:
> def fac(n): return 1 if n==0 else n * fac(n-1) > def choose(n,k): return fac(n) / fac(k) / fac(n-k) > def prob(n,k,p): return choose(n,k) * p ** k * (1-p) ** (n-k)
The last formula computes the probability that exactly k servers out of n will be online if each individual server has a probability p of being online. Now, we’ll do:
> sum((prob(60, k, 0.5) for k in range(0, 20))) 0.0031088013296633353
99.7% uptime with only 3x redundancy – a good step up from the 87.5% uptime that 3x redundancy would have given us had simple replication been the only tool in our toolkit. If we crank the redundancy up to 4x, then we get six nines, and we can stop there because the probability either Ethereum or the entire internet will crash outright is greater than 0.0001% anyway (in fact, you’re more likely to die tomorrow). Oh, and if we assume each machine has 90% uptime (ie. hobbyist “farmers”), then with a 1.5x-redundant 20-of-30 protocol we get an absolutely overkill twelve nines. Reputation systems can be used to keep track of how often each node is online.
Dealing with Errors
We’ll spend the rest of this article discussing three extensions to this scheme. The first is a concern that you may have skipped over reading the above description, but one which is nonetheless important: what happens if some node tries to actively cheat? The algorithm above can recover the original data of a 20-of-60 split from any 20 pieces, but what if one of the data providers is evil and tries to provide fake data to screw with the algorithm. The attack vector is a rather compelling one:
> share.lagrange_interp((1.0, 3.0, 2.0, 5.0), (1.0, 2.0, 3.0, 4.0)) (-11.0, 19.333333333333336, -8.5, 1.1666666666666665)
Taking the four points of the above polynomial, but changing the last value to 5, gives a completely different result. There are two ways of dealing with this problem. One is the obvious way, and the other is the mathematically clever way. The obvious way is obvious: when splitting a file, keep the hash of each chunk, and compare the chunk against the hash when receiving it. Chunks that do not match their hashes are to be discarded.
The clever way is somewhat more clever; it involves some spooky not-quite-moon-math called the Berlekamp-Welch algorithm. The idea is that instead of fitting just one polynomial, P, we imagine into existence two polynomials, Q and E, such that Q(x) = P(x) * E(x), and try to solve for both Q and E at the same time. Then, we compute P = Q / E. The idea is that if the equation holds true, then for all x either P(x) = Q(x) / E(x) or E(x) = 0; hence, aside from computing the original polynomial we magically isolate what the errors are. I won’t go into an example here; the Wikipedia article has a perfectly decent one, and you can try it yourself with:
> map(lambda x: share.eval_poly_at((-7.0, 12.0, -4.5, 0.5), x), (1, 2, 3, 4, 5, 6)) (1.0, 3.0, 2.0, 1.0, 3.0, 11.0) > share.berlekamp_welch_attempt((1.0, 3.0, 18018.0, 1.0, 3.0, 11.0), (1, 2, 3, 4, 5, 6), 3) (-7.0, 12.0, -4.5, 0.5) > share.berlekamp_welch_attempt((1.0, 3.0, 2.0, 1.0, 3.0, 0.0), (1, 2, 3, 4, 5, 6), 3) (-7.0, 12.0, -4.5, 0.5)
Now, as I mentioned, this mathematical trickery is not really all that needed for file storage; the simpler approach of storing hashes and discarding any piece that does not match the recorded hash works just fine. But it is incidentally quite useful for another application: self-healing Bitcoin addresses. Bitcoin has a base58check encoding algorithm, which can be used to detect when a Bitcoin address has been mistyped and returns an error so you do not accidentally send thousands of dollars into the abyss. However, using what we know, we can actually do better and make an algorithm which not only detects mistypes but also actually corrects the errors on the fly. We don’t use any kind of clever address encoding for Ethereum because we prefer to encourage use of name registry-based alternatives, but if an address encoding scheme was demanded something like this could be used.
Finite Fields
Now, we get back to the second problem: once our x coordinates get a little higher, the y coordinates start shooting off very quickly toward infinity. To solve this, what we are going to do is nothing short of completely redefining the rules of arithmetic as we know them. Specifically, let’s redefine our arithmetic operations as:
a + b := (a + b) % 11 a - b := (a - b) % 11 a * b := (a * b) % 11 a / b := (a * b ** 9) % 11
That “percent” sign there is “modulo”, ie. “take the remainder of dividing that vaue by 11”, so we have
7 + 5 = 1,
6 * 6 = 3(and its corollary
3 / 6 = 6), etc. We are now only allowed to deal with the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. The surprising thing is that, even as we do this, all of the rules about traditional arithmetic still hold with our new arithmetic;
(a * b) * c = a * (b * c),
(a + b) * c = (a * c) + (b * c),
a / b * b = aif
b != 0,
(a^2 - b^2) = (a - b)*(a + b), etc. Thus, we can simply take the algebra behind our polynomial encoding that we used above, and transplant it over into the new system. Even though the intuition of a polynomial curve is completely borked – we’re now dealing with abstract mathematical objects and not anything resembling actual points on a plane – because our new algebra is self-consistent, the formulas still work, and that’s what counts.
> e = share.mkModuloClass(11) > P = share.lagrange_interp(map(e, (1, 3, 2, 1)), map(e, (1, 2, 3, 4))) > P (4, 1, 1, 6) > map(lambda x: share.eval_poly_at(map(e, P), e(x)), range(1, 9)) (1, 3, 2, 1, 3, 0, 6, 2) > share.berlekamp_welch_attempt(map(e, (1, 9, 9, 1, 3, 0, 6, 2)), map(e, (1, 2, 3, 4, 5, 6, 7, 8)), 3) (4, 1, 1, 6)
The “
map(e, (v1, v2, v3))” is used to convert ordinary integers into elements in this new field; the software library includes an implementation of our crazy modulo 11 numbers that interfaces with arithmetic operators seamlessly so we can simply swap them in (eg.
print e(6) * e(6)returns
3). You can see that everything still works – except that now, because our new definitions of addition, subtraction, multiplication and division always return integers in
(0 ... 10) we never need to worry about either floating point imprecision or the numbers expanding as the x coordinate gets too high.
Now, in reality these relatively simple modulo finite fields are not what are usually used in error-correcting codes; the generally preferred construction is something called a Galois field (technically, any field with a finite number of elements is a Galois field, but sometimes the term is used specifically to refer to polynomial-based fields as we will describe here). The idea is that the elements in the field are now polynomials, where the coefficients are themselves values in the field of integers modulo 2 (ie. a + b := (a + b) % 2, etc). Adding and subtracting work as normally, but multiplying is itself modulo a polynomial, specifically x^8 + x^4 + x^3 + x + 1. This rather complicated multilayered construction lets us have a field with exactly 256 elements, so we can conveniently store every element in one byte and every byte as one element. If we want to work on chunks of many bytes at a time, we simply apply the scheme in parallel (ie. if each chunk is 1024 bytes, determine 10 polynomials, one for each byte, extend them separately, and combine the values at each x coordinate to get the chunk there).
But it is not important to know the exact workings of this; the salient point is that we can redefine +, –, * and / in such a way that they are still fully self-consistent but always take and output bytes.
Going Multidimensional: The Self-Healing Cube
Now, we’re using finite fields, and we can deal with errors, but one issue still remains: what happens when nodes do go down? At any point in time, you can count on 50% of the nodes storing your file staying online, but what you cannot count on is the same nodes staying online forever – eventually, a few nodes are going to drop out, then a few more, then a few more, until eventually there are not enough of the original nodes left online. How do we fight this gradual attrition? One strategy is that you could simply watch the contracts that are rewarding each individual file storage instance, seeing when some stop paying out rewards, and then re-upload the file. However, there is a problem: in order to re-upload the file, you need to reconstruct the file in its entirety, a potentially difficult task for the multi-gigabyte movies that are now needed to satisfy people’s seemingly insatiable desires for multi-thousand pixel resolution. Additionally, ideally we would like the network to be able to heal itself without requiring active involvement from a centralized source, even the owner of the files.
Fortunately, such an algorithm exists, and all we need to accomplish it is a clever extension of the error correcting codes that we described above. The fundamental idea that we can rely on is the fact that polynomial error correcting codes are “linear”, a mathematical term which basically means that it interoperates nicely with multiplication and addition. For example, consider:
> share.lagrange_interp((1.0, 3.0, 2.0, 1.0), (1.0, 2.0, 3.0, 4.0)) (-7.0, 12.000000000000002, -4.5, 0.4999999999999999) > share.lagrange_interp((10.0, 5.0, 5.0, 10.0), (1.0, 2.0, 3.0, 4.0)) (20.0, -12.5, 2.5, 0.0) > share.lagrange_interp((11.0, 8.0, 7.0, 11.0), (1.0, 2.0, 3.0, 4.0)) (13.0, -0.5, -2.0, 0.5000000000000002) > share.lagrange_interp((22.0, 16.0, 14.0, 22.0), (1.0, 2.0, 3.0, 4.0)) (26.0, -1.0, -4.0, 1.0000000000000004)
See how the input to the third interpolation is the sum of the inputs to the first two, and the output ends up being the sum of the first two outputs, and then when we double the input it also doubles the output. So what’s the benefit of this? Well, here’s the clever trick. Erasure cording is itself a linear formula; it relies only on multiplication and addition. Hence, we are going to apply erasure coding to itself. So how are we going to do this? Here is one possible strategy.
First, we take our 4-digit “file” and put it into a 2×2 grid.
Then, we use the same polynomial interpolation and extension process as above to extend the file along both the x and y axes:
1 3 5 7 2 1 0 10 3 10 4 8
And then we apply the process again to get the remaining 4 squares:
1 3 5 7 2 1 0 10 3 10 6 2 4 8 1 5
Note that it doesn’t matter if we get the last four squares by expanding horizontally and vertically; because secret sharing is linear it is commutative with itself, so you get the exact same answer either way. Now, suppose we lose a number in the middle, say, 6. Well, we can do a repair vertically:
> share.repair((5, 0, None, 1), e) (5, 0, 6, 1)
Or horizontally:
> share.repair((3, 10, None, 2), e) (3, 10, 6, 2)
And tada, we get 6 in both cases. This is the surprising thing: the polynomials work equally well on both the x or the y axis. Hence, if we take these 16 pieces from the grid, and split them up among 16 nodes, and one of the nodes disappears, then nodes along either axis can come together and reconstruct the data that was held by that particular node and start claiming the reward for storing that data. Ideally, we can even extend this process beyond 2 dimensions, producing a 3-dimensional cube, a 4-dimensional hypercube or more – the gain of using more dimensions is ease of reconstruction, and the cost is a lower degree of redundancy. Thus, what we have is an information-theoretic equivalent of something that sounds like it came straight out of science-fiction: a highly redundant, interlinking, modular self-healing cube, that can quickly locally detect and fix its own errors even if large sections of the cube were to be damaged, co-opted or destroyed.

“The cube can still function even if up to 78% of it were to be destroyed…”
So, let’s put it all together. You have a 10 GB file, and you want to split it up across the network. First, you encrypt the file, and then you split the file into, let’s say, 125 chunks. You arrange these chunks into a 3-dimensional 5x5x5 cube, figure out the polynomial along each axis, and “extend” each one so that at the end you have a 7x7x7 cube. You then look for 343 nodes willing to store each piece of data, and tell each node only the identity of the other nodes that are along the same axis (we want to make an effort to avoid a single node gathering together an entire line, square or cube and storing it and calculating any redundant chunks as needed in real-time, getting the reward for storing all the chunks of the file without actually providing any redundancy.
In order to actually retrieve the file, you would send out a request for all of the chunks, then see which of the pieces coming in have the highest bandwidth. You may use the pay-per-chunk protocol to pay for the sending of the data; extortion is not an issue because you have such high redundancy so no one has the monopoly power to deny you the file. As soon as the minimal number of pieces arrive, you would do the math to decrypt the pieces and reconstitute the file locally. Perhaps, if the encoding is per-byte, you may even be able to apply this to a Youtube-like streaming implementation, reconstituting one byte at a time.
In some sense, there is an unavoidable tradeoff between self-healing and vulnerability to this kind of fake redundancy: if parts of the network can come together and recover a missing piece to provide redundancy, then a malicious large actor in the network can recover a missing piece on the fly to provide and charge for fake redundancy. Perhaps some scheme involving adding another layer of encryption on each piece, hiding the encryption keys and the addresses of the storers of the individual pieces behind yet another erasure code, and incentivizing the revelation process only at some particular times might form an optimal balance.
Secret Sharing
At the beginning of the article, I mentioned another name for the concept of erasure coding, “secret sharing”. From the name, it’s easy to see how the two are related: if you have an algorithm for splitting data up among 9 nodes such that 5 of 9 nodes are needed to recover it but 4 of 9 can’t, then another obvious use case is to use the same algorithm for storing private keys – split up your Bitcoin wallet backup into nine parts, give one to your mother, one to your boss, one to your lawyer, put three into a few safety deposit boxes, etc, and if you forget your password then you’ll be able to ask each of them individually and chances are at least five will give you your pieces back, but the individuals themselves are sufficiently far apart from each other that they’re unlikely to collude with each other. This is a very legitimate thing to do, but there is one implementation detail involved in doing it right.
The issue is this: even though 4 of 9 can’t recover the original key, 4 of 9 can still come together and have quite a lot of information about it – specifically, four linear equations over five unknowns. This reduces the dimensionality of the choice space by a factor of 5, so instead of 2256 private keys to search through they now have only 251. If your key is 180 bits, that goes down to 236 – trivial work for a reasonably powerful computer. The way we fix this is by erasure-coding not just the private key, but rather the private key plus 4x as many bytes of random gook. More precisely, let the private key be the zero-degree coefficient of the polynomial, pick four random values for the next four coefficients, and take values from that. This makes each piece five times longer, but with the benefit that even 4 of 9 now have the entire choice space of 2180 or 2256 to search through.
Conclusion
So there we go, that’s an introduction to the power of erasure coding – arguably the single most underhyped set of algorithms (except perhaps SCIP) in computer science or cryptography. The ideas here essentially are to file storage what multisig is to smart contracts, allowing you to get the absolutely maximum possible amount of security and redundancy out of whatever ratio of storage overhead you are willing to accept. It’s an approach to file storage availability that strictly supersedes the possibilities offered by simple splitting and replication (indeed, replication is actually exactly what you get if you try to apply the algorithm with a 1-of-n strategy), and can be used to encapsulate and separately handle the problem of redundancy in the same way that encryption encapsulates and separately handles the problem of privacy.
Decentralized file storage is still far from a solved problem; although much of the core technology, including erasure coding in Tahoe-LAFS, has already been implemented, there are certainly many minor and not-so-minor implementation details that still need to be solved for such a setup to actually work. An effective reputation system will be required for measuring quality-of-service (eg. a node up 99% of the time is worth at least 3x more than a node up 50% of the time). In some ways, incentivized file storage even depends on effective blockchain scalability; having to implicitly pay for the fees of 343 transactions going to verification contracts every hour is not going to work until transaction fees become far lower than they are today, and until then some more coarse-grained compromises are going to be required. But then again, pretty much every problem in the cryptocurrency space still has a very long way to go.

