In our previous article, Quantum Supremacy: Is it a Real Threat?, we looked at how quantum computers pose an existential threat to modern cryptography. RSA, elliptic curve cryptography, and most of the cryptographic systems that secure the digital world today rely on computational problems that quantum algorithms can solve exponentially faster than classical computers.
However, there are still mathematical approaches that remain unwavering despite quantum advances. Shamir’s Secret Sharing (SSS) Secret distribution or key splitting method. It is based on classical information theory and polynomial interpolation, rather than number theory assumptions (such as factorization or discrete logarithms) that quantum computers break.
This makes it not directly susceptible to quantum attacks like Shor’s algorithm.
Two types of security
Most encryption today uses: computer security. This means that the system is safe as long as the specific mathematical problem is difficult to solve within a reasonable time limit. RSA depends on the difficulty of factoring large integers. Elliptic curve cryptography relies on the complexity of the discrete logarithmic problem. This assumption works well for classical computers, but fails for quantum algorithms such as Shor’s algorithm.
Information-theoretic security It takes a completely different approach. Instead of relying on computational robustness, security is achieved through mathematical impossibility. When Claude Shannon introduced this concept in 1949, he proved that some systems are mathematically secure against all attackers, regardless of their computational power.
Disposable pads are a classic example. If the encryption key were truly random, it would be mathematically indecipherable as long as the message was used only once. This holds despite infinite computing power. An attacker viewing an encrypted message will only see random data, with no way to distinguish the correct decryption from other possible messages of the same length.
Shamir’s Secret Sharing achieves this same level of mathematical certainty through a different mechanism. polynomial math.
Polynomial Interpolation – Unbreakable Security
Adi Shamir’s 1979 innovation is based on the fundamental properties of polynomials. N Points that determine degree polynomial N-1 peculiarly. If this sounds familiar, think back to high school geometry. Every straight line is uniquely determined by two points. With just one point, an infinite number of lines can pass through that point. This is actually the basic principle behind the 2/3 method, which is the most common Shamir threshold. here, N is 2, so the polynomial is a linear equation, which is the equation for a straight line. This simple mathematical fact is the basis of a security model that is not only provable but also inherently quantum-resistant. This means that if an attacker has only one share (the coordinates of a single point), they cannot reconstruct the secret “line”. As a result, there are infinitely many equally plausible secrets for them to consider.
Below is a basic example of the concepts described above.
- secret s = 6. Select a random line → Y = 5x + 6
- Create two shares:
- At first x = 1 → Y = 11 → (1, 11);
- second time x = 3 → Y = 21 → (3, 21).
- Reconstruct:
- slope a = (21 − 11) / (3 − 1) = 5;
- then y = 5x + bplug x = 1, y = 11 → b = 6.
- The secret is value. x = 0: y(0) = 6 — I have recovered.
Here more complex official t-of-n generalization example:
Secret as the value of a 0 degree (t−1) polynomial:
Create share: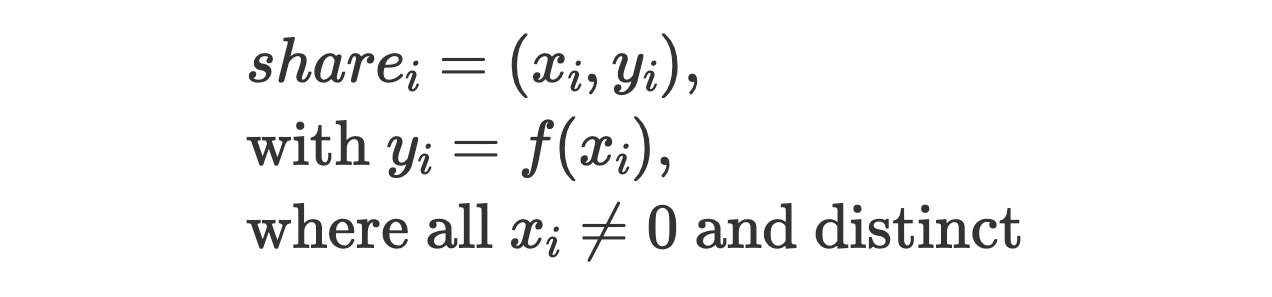
Secret reconstruction (Lagrange at x=0):
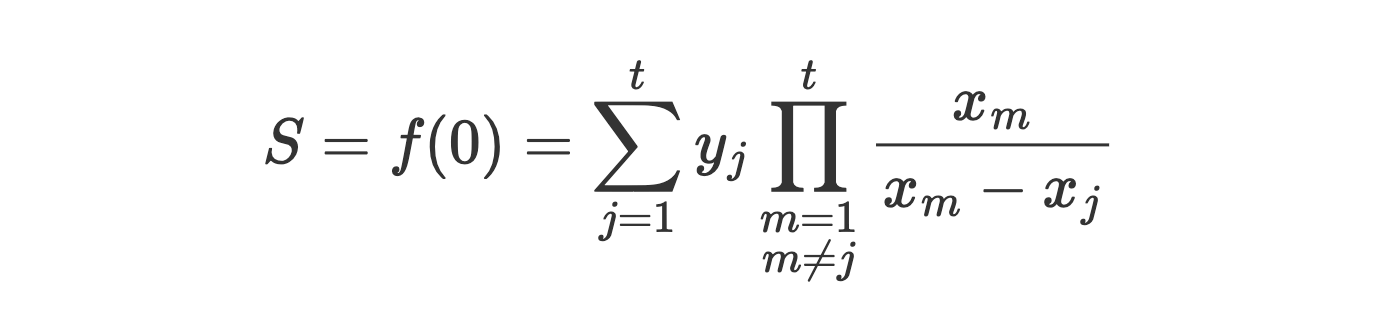
security proof
If there are only t-1 shares, there are t-1 equations, but there are t unknowns (t coefficients of the polynomial). In linear algebra, this system has an infinite number of solutions. All possible secret values occur equally given the available information.
This is not a computational limitation, but a mathematical impossibility. Even if we know that t-1 shares perfectly, an attacker with a quantum computer and unlimited time would not be able to determine which of the infinite possible secrets is correct.
Why quantum computers can’t break information theory security
Quantum computers excel at certain types of problems through quantum properties such as superposition and entanglement. Shor’s algorithm can factor integers exponentially faster than conventional computers. Grover’s algorithm can search unsorted databases with a quadratic speedup.
However, quantum computers cannot violate fundamental mathematical constraints. If a polynomial of order t-1 requires t points for its unique determination, no amount of quantum computation can extract more information from fewer points. The security of Shamir’s secret sharing is based not on computational difficulty but on mathematical impossibility.
This creates an interesting paradox. Quantum computers will destroy the RSA, AES, and elliptic curve systems that protect most digital infrastructure, but they will still be powerless against systems invented using classical mathematics in 1979.
Inherited Immunity: Building Quantum Resistance Systems Using Thresholds
Shamir’s quantum resistance to secret sharing isn’t just a feature of the algorithm itself. It is also a property that can be inherited by any system built on top of it. This makes SSS a powerful foundation for creating complex, quantum-resilient security models based on distributed trust.
At its core (T, N) The threshold scheme is more than just a way to partition secrets. This is a mechanism for decentralizing authority and eliminating single points of failure. When a large-scale system uses SSS to protect sensitive secrets, the core secret management layer of that system inherits the information-theoretic security of SSS. This allows the design of sophisticated quantum-resistant access control systems.
This approach is excellent for protecting sensitive secrets that require long-term protection and distributed access control, such as:
- Fault-tolerant backup Cryptocurrency wallet seed phrase and private key.
- protect Certification Authority Root Key.
- security database encryption key.
- Guard ring corporate trade secrets and intellectual property.
- Military and Critical Infrastructure Secrets like nuclear launch codes.
This model is used in the following applications: Vault 12 GuardProvides a quantum-resistant method for personal disaster recovery and digital inheritance. Mathematics is also expanded effectively. Increasing the threshold does not cause an exponential increase in computational requirements like many cryptographic systems do. Polynomial order increases linearly with threshold, maintaining practical performance even in large-scale deployments.
Comparing SSS to traditional encryption under quantum threats
| side | traditional cryptocurrency | Sharing Shamir’s Secret |
|---|---|---|
| security foundation | computerized hardness | mathematical impossibility |
| quantum vulnerability | Vulnerable to Shor’s algorithm | adoptive immunity |
| key management | single point of failure | distributed trust |
| Performance Impact | Quantum attacks weaken security | No impact from quantum power generation |
| future proof | Algorithm update required | inherently forward-looking |
Practical Considerations and Implementation Challenges
SSS is perfect in theory, but practical implementation requires careful design.
- Secure Share Distribution: The shares themselves must be distributed and stored safely. If you send a share using a quantum vulnerable channel, the overall security of your system may be compromised. This is why protocols like the hardened, open-source Zax Relay are critical to transport.
- stock protection: Each stock must be protected against theft or loss. Encrypting shares with existing algorithms can re-introduce quantum vulnerabilities. A better approach is to leverage hardware security, such as Secure Enclave on smartphones, to protect shares at rest. Vault 12 Guard The app is like that.
- Use secure secrets: SSS protects your stored secrets. Once reconstructed, the secret must be used safely. In Bitcoin, it is recommended to use Taproot addresses (starting with ‘bc1p’) for maximum quantum resilience. This is because the 256-bit key structure of Taproot addresses provides stronger protection against quantum search algorithms than the 160-bit hashes of previous address types. Most importantly, Never reuse addresses This is an important security practice. After funds are spent from an address, the public key is exposed, making it a potential target for quantum threats.
SSS and Postquantum Cryptography: Hybrid Defense
A race to standardize post-quantum cryptography (PQC) is underway, led by organizations such as NIST. These efforts have resulted in next-generation algorithms designed to withstand quantum attacks, such as CRYSTALS-Kyber (for key encapsulation) and CRYSTALS-Dilithium (for digital signatures). Alongside this, other powerful primitives, such as the hash-based signature scheme SPHINCS+ (specified in IETF RFC 8391), provide proven support for conservative security.
However, it is important to understand that although these new PQC algorithms are powerful, they still operate according to the following principles: computer security. It is based on a mathematical problem that is considered difficult for both classical and quantum computers. They represent the next frontier in the long-term arms race, but they do not provide the conclusion to this race.
This is where Shamir’s secret sharing provides a perfect, complementary layer of defense. SSS does not compete with PQC. We work together to create a truly hybrid defense-in-depth architecture.
You can use PQC algorithms to do what they do best: secure data in transit, authenticate, and digitally sign. You can then utilize SSS to secure your ultimate “Keys to the Kingdom”. This creates a powerful hybrid model. Even if future theoretical or computational innovations break today’s PQC standards, the core secrets protected by SSS will remain safe due to information-theoretic guarantees. It is the ultimate backstop for an uncertain future.
Timeless solutions for future threats
As quantum computing advances, organizations will need an encryption strategy that provides both immediate protection and long-term security assurance. SSS offers a unique value proposition: mathematical certainty in an uncertain technological future.
In the next article, “Building Quantum Resistance Apps Using Capacitors,” we will look at practical implementation strategies for integrating SSS into modern applications. It covers the Capacitor plug-in ecosystem, performance optimization techniques, and real-world deployment patterns that combine theoretical security guarantees with real-world usability.
The quantum threat is real and looming. But using mathematical tools like Shamir’s secret sharing, we can build systems that will remain secure regardless of future technological advancements. The mathematics discovered by Shamir in 1979 provide a timeless foundation for security in the quantum age.